Stelling van Pythagoras
De Stelling van Pythagoras is een formule uit de wiskunde. In rekentaal ziet de stelling van Pythagoras er zo uit:
a2 + b2 = c2
Dat spreek je zo uit:
a in het kwadraat plus b in het kwadraat is c in het kwadraat.
De letters a, b en c staan allemaal voor één van de zijde van een speciale driehoek. a2, b2 en c2 staan voor de lengtes van de zijdes van de drie vierkanten die je in de tekening ziet. De stelling zegt dat de oppervlakte van vierkant a plus de oppervlakte van vierkant b bij elkaar net zo groot zijn als het oppervlakte van vierkant c. In een vierkant kun je de oppervlakte uitrekenen door het kwadraat te nemen van de lengte van een zijde van het vierkant.
Speciaal aan de driehoek is dat één van de hoeken van de driehoek precies negentig graden is, zoals je dat in een rechthoek ook hebt. Je noemt zo'n driehoek daarom ook een rechthoekige driehoek.
De stelling geeft aan dat als je de lengte van zijde a weet en de lengte van zijde b weet, je dan de lengte van zijde c kunt uitrekenen.
Stel je weet het volgende:
- de lengte van zijde a is drie centimeter
- de lengte van zijde b is vier centimeter
Dan kun je met de stelling van Pythagoras uitrekenen hoe lang zijde c precies is.
32 + 42 = c2
- drie in het kwadraat is negen
- vier in het kwadraat is zestien
Dan staat er dus het volgende
9 + 16 = c2
negen plus zestien is vijfentwintig. Dan staat er dus:
25 = c2
Je kunt dus zeggen dat c in het kwadraat gelijk is aan vijfentwintig. Om c zelf uit te rekenen moet je de wortel trekken van c2. De wortel van vijfentwintig is vijf.
5 = c
De lengte van zijde c is dus vijf.
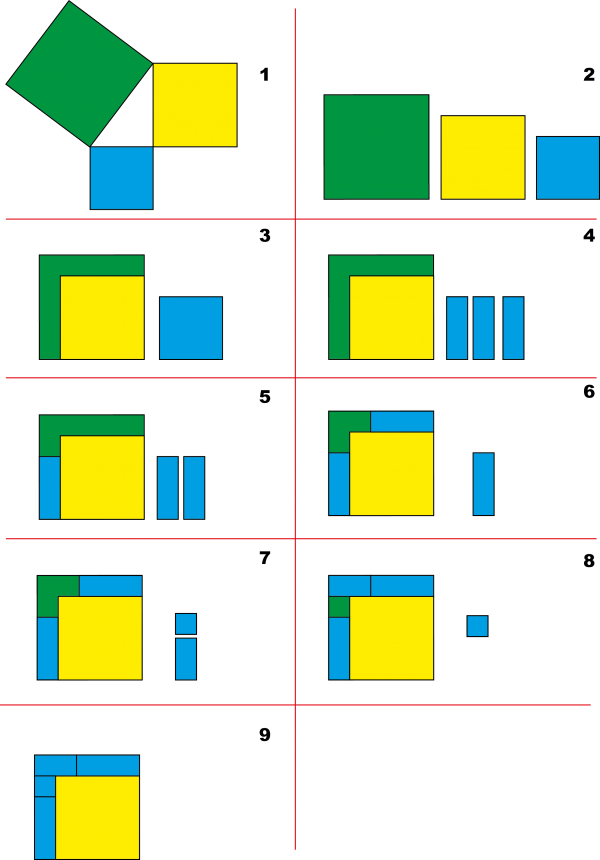
Bewijs voor de stelling van Pythagoras
Hiernaast zie je negen plaatjes die laten zien dat het klopt dat de oppervlakte van het vierkant aan de schuine zijde even groot is als de oppervlakten van de vierkanten aan de rechte zijden.